Indicateurs de vitesse aux graphiques Smith

Compteurs de vitesse, thermomètres, compteurs SWR et graphiques Smith

Vous êtes-vous déjà demandé ce que ces quatre choses ont en commun ? Non, bien sûr que non, moi non plus ! Mais peut-être vous êtes- vous demandé pourquoi un graphique de Smith a des lignes de grille aussi étranges. Croyez-le ou non, il existe une progression logique des compteurs de vitesse aux graphiques Smith qui rendra la grille Smith limpide.

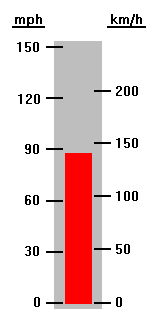
	Ce sont des images stylisées d'un compteur de vitesse et d'un thermomètre. Le compteur de vitesse indique une vitesse qui vous rapportera tôt ou tard une contravention. Le thermomètre peut indiquer la température d'une tasse de café. Le compteur de vitesse est marqué à la fois en miles par heure et en kilomètres par heure. Les marques ne sont pas alignées, ce qui permet d'utiliser de jolis chiffres ronds sur les deux échelles. Sur le thermomètre, les marques sont alignées mais les nombres Fahrenheit ont évidemment été forcés de correspondre à l'échelle Celsius. Peu importe comment les échelles sont marquées. Pour la vitesse et la température, une seule quantité est mesurée, mais la mesure est alors affichée avec deux échelles différentes.

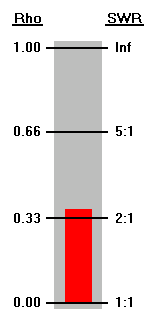
	Il s'agit d'un compteur SWR. Ces compteurs ne mesurent pas réellement le rapport d'ondes stationnaires. Ils mesurent l'amplitude du coefficient de réflexion (rho) par rapport à une référence donnée, généralement 50 ohms. L'échelle peut être indiquée en unités SWR, mais il est important de se rappeler que l'échelle "réelle" (mais peut-être non représentée) est l'amplitude du coefficient de réflexion. Le compteur SWR ne concerne que l' amplitude du coefficient de réflexion, mais rho est une quantité complexe ayant à la fois une amplitude et un angle. Si rho devait être mesuré à divers points le long d'une ligne de transmission, la magnitude serait assez constante mais l'angle changerait en fonction de la longueur électrique de la ligne au point de mesure.

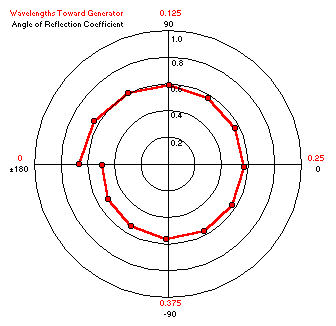
Ce graphique montre à la fois l'amplitude rho et l'angle rho aux points le long d'une section de ½ longueur d'onde du RG-174 à 3,75 MHz. La ligne se termine avec une charge de 10+j0 ohms. Les calculs ont été effectués tous les 15 degrés électriques dans le sens des aiguilles d'une montre vers l'extrémité du générateur de la ligne. La magnitude Rho est indiquée par la distance depuis le centre du graphique et l'angle Rho est mesuré à partir de la position 3 heures.

Parce que RG-174 est une ligne avec perte, le tracé a la forme d'une spirale plutôt que d'un cercle. L'amplitude du coefficient de réflexion diminue sensiblement à mesure que la distance à la charge augmente. L'amplitude de Rho à la charge est de 0,667 (SWR 5: 1) alors qu'après ½ longueur d'onde, elle est tombée à 0,494 (SWR 2,95: 1). L'angle rhô commence à (environ) 180° et balaie un cercle entier pour revenir à (environ) 180°.

( Pourquoi environ ? )

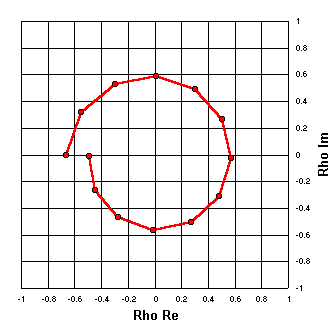
La quantité complexe rho peut être exprimée sous forme de composantes réelles et imaginaires au lieu de grandeur et d'angle. Les marques d'échelle sur le tracé de gauche l'indiquent, mais notez que la forme de la spirale est exactement la même que sur le tracé précédent. Ceci est analogue aux exemples de compteur de vitesse et de thermomètre, où la même quantité peut être indiquée avec différentes échelles.

La vitesse et la température sont bien sûr des grandeurs scalaires qui peuvent être exprimées par un seul nombre. Rho est une quantité vectorielle qui nécessite deux nombres pour être complètement définie. Essayer de mettre les deux ensembles d'échelles sur le même graphique serait déroutant, mais l'idée est la même.

R = 0

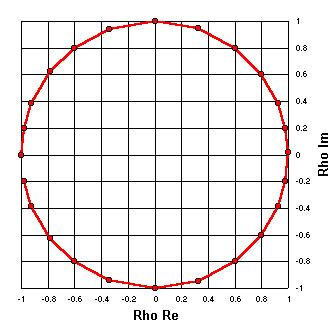
Au lieu de tracer les coefficients de réflexion comme on le trouverait le long d'une ligne de transmission, nous pouvons tracer les coefficients de réflexion qui correspondent à des valeurs d'impédance arbitraires. Pour toute impédance complexe arbitraire Z (R±jX), le coefficient de réflexion peut être calculé comme

Rho = (Z - Z réf ) / (Z + Z réf )

Dans ce graphique, toutes les valeurs Z arbitraires ont une résistance de R = 0 ohms. Les valeurs de réactance sont X = 0, 5, 10, 17, 25, 35, 50, 70, 100, 150, 250, 500, 5000, -500, -250, ... , -10 et -5. (C'est-à-dire, Z = 0+j0, 0+j5, 0+j10, etc.) Une impédance de référence (Z ref ) d'exactement 50+j0 ohms a été utilisée pour ce tableau et pour tous les autres tableaux de cette page.

R = 10

Maintenant, ce processus sera répété, mais cette fois, la composante R des points Z arbitraires sera de 10 ohms. Le tableau suivant montre quelques-uns des calculs.

Étiqueter Z arbitraire Rho Ré Rho je suis

UN 10 + j 0 -0,667 0

B 10 +j 10 -0,622 +0,270

C 10 + j 50 +0,016 +0,820

D 10 +j 500 +0,976 +0,197

E 10 -j 50 +0,016 -0,820

Rho Z réf = 50 +j 0

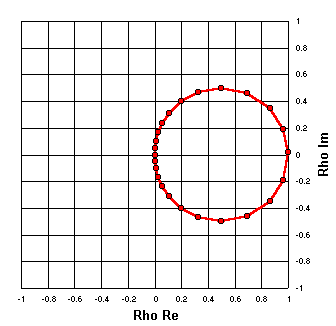
R = 50

Et encore, mais avec R égal à 50 ohms. (Z = 50+j0, 50+j5, 50+j10, etc.)

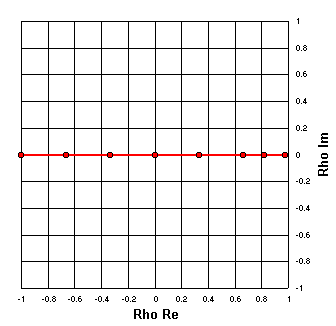
X = 0

Traçons maintenant les composantes réelles et imaginaires des coefficients de réflexion à partir d'un ensemble de valeurs Z arbitraires avec la composante X maintenue constante. Dans ce cas R = 0, 10, 25, 50, 100, 250, 500, 5000 et X est maintenu constant à 0.

X = ±10

Vous avez l'idée, alors montrons maintenant deux ensembles de tracés. L'arc supérieur correspond à R = 0, 10, 25, 50, 100, 250, 500 avec X = 10, et l'arc inférieur correspond au même ensemble de valeurs R mais avec X = -10.

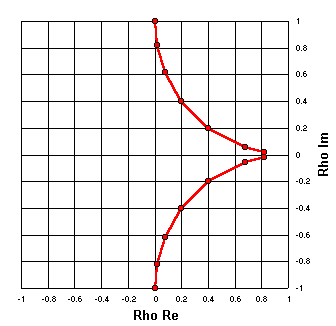
X = ±50

Une dernière fois. Même ensemble de valeurs R que dans le graphique précédent, avec X = 50 et X = -50.

Voici les six graphiques précédents superposés , avec des étiquettes pour indiquer quelle composante des valeurs Z arbitraires a été maintenue constante.

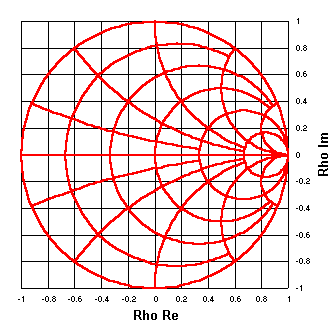
Nous avons maintenant ajouté quelques points supplémentaires à chacun des tracés précédents et supprimé les marqueurs de points individuels afin de lisser les courbes. Nous avons également ajouté des tracés pour R maintenu constant à 25, 100 et 250 ohms avec X variable, et pour X maintenu constant à ±25, ±100 et ±250 ohms avec R variable.

Maintenant, les lignes de grille et les étiquettes Rho Re et Rho Im ont été masquées. Les lignes de tracé rouges épaisses ont été remplacées par des lignes de "grille" noires claires et des étiquettes ont été ajoutées pour afficher les valeurs R ou X constantes qui ont été utilisées pour créer chaque ligne.

Notez que ce tableau, tout comme le compteur SWR, est toujours basé sur les coefficients de réflexion. Mais maintenant, au lieu des échelles de graphique montrant la magnitude et l'angle rho, ou les composantes réelles et imaginaires rho, elles affichent les valeurs d'impédance (R et X) pour une base de référence de 50 ohms. C'est exactement comme ajouter une troisième échelle au thermomètre, peut-être des degrés Kelvin, puis effacer les échelles Celsius et Fahrenheit. L'instrument mesurerait toujours la température et vous l'appelleriez toujours un "thermomètre".

Le tableau de gauche pourrait s'appeler un "tableau de coefficient de réflexion avec des marques d'échelle d'impédance", mais la plupart des gens choisissent plutôt d'honorer son inventeur et l'appellent un tableau de Smith.

(Passez la souris sur n'importe quel marqueur rouge.)
(Peut ne pas fonctionner avec certains navigateurs.)

Vous souvenez-vous de l'exemple de la ligne de transmission RG-174 avec des calculs effectués tous les 15 degrés électriques ? Le même tracé est illustré à gauche, mais avec des marques d'échelle en termes de valeurs d'impédance aux points le long de la ligne plutôt que des valeurs de coefficient de réflexion. Remarquez que la forme de la spirale est exactement la même. Si vous ne me croyez pas, cliquez simplement sur l'un des boutons.

Passez le pointeur de votre souris sur n'importe quel marqueur rouge pour voir les valeurs exactes de ce point, affichées soit sur la ligne d'état, soit dans une fenêtre contextuelle en fonction de votre navigateur. (Peut ne pas fonctionner avec certains navigateurs.)
( Quelle est la précision de ces graphiques ? )

Et juste pour une perspective historique, cliquez ici pour voir les mêmes points tracés sur un graphique similaire au graphique "précurseur" de Smith, vers 1931.

Home