Un système d'antenne populaire, en particulier sur les bandes HF inférieures, se compose de plusieurs éléments, tous pilotés directement via des lignes d'alimentation. Une mise en œuvre d'un tel système utilise des lignes de différentes longueurs pour fournir l'amplitude et la phase de courant appropriées à chaque élément. Cette section explique comment utiliser Zplots pour "voir" ce qui se passe le long des lignes.
L'exemple utilisé est un modèle EZNEC d'un simple réseau cardioïde à deux éléments à 7,15 MHz et est discuté plus en détail dans le chapitre 8 des éditions récentes de The ARRL Antenna Book . Chaque élément est une verticale quart d'onde montée au sol, espacée d'un quart de longueur d'onde, alimentée par des courants d'amplitude égale mais déphasés de 90 °. Les éléments mesurent 33 pieds de haut et seraient auto-résonnants (ont une réactance nulle) s'ils fonctionnaient isolément. Plutôt que de modéliser directement les radiales enterrées (ce qui nécessiterait l'utilisation d'un moteur NEC-4), un sol de type Real/MININEC est utilisé et une charge forfaitaire est ajoutée à la base de chaque élément. Pour simuler l'effet approximatif de 8 radiales enterrées, la valeur de charge est de 18 ohms. Cela ajoute 18 ohms de résistance de perte en série avec la résistance de rayonnement de l'élément.
Les panneaux EZNEC pertinents sont présentés ci-dessous.
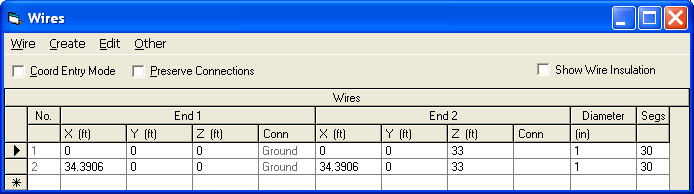

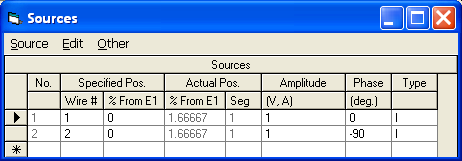
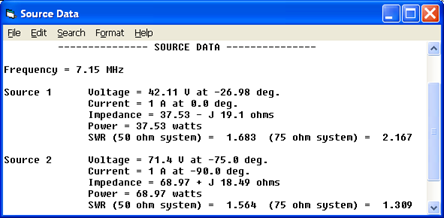
Notez que si l'un ou l'autre des éléments fonctionnait indépendamment, l'impédance de la source serait d'environ 54 + 10 ohms, une combinaison de 36 ohms de résistance au rayonnement et de 18 ohms de perte à la terre. En raison du couplage mutuel entre les éléments, les deux impédances de source diffèrent de cette valeur, et parce que les éléments sont déphasés de 90°, les impédances de source diffèrent l'une de l'autre.
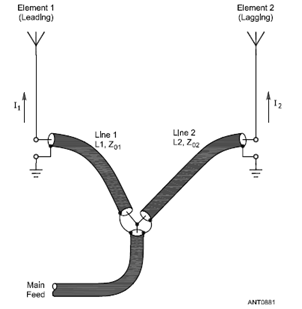
Le modèle initial utilise des sources de courant idéales à la base de chaque élément pour fournir l'amplitude et la phase de courant correctes. Mais le but ultime est d'alimenter les éléments via des lignes de différentes longueurs à partir d'une jonction commune tout en fournissant des courants de même amplitude et déphasés à 90°. Ceci est montré à gauche dans une illustration de The ARRL Antenna Book (Fig 16 aux pages 8-18 de la 21e édition). Pour des raisons non couvertes ici, les retards de phase introduits par les lignes d'alimentation séparées (Ligne 1 et Ligne 2 dans l'illustration) ne sont pas égaux aux longueurs électriques de la ligne. Autrement dit, vous ne pouvez pas simplement allonger la ligne 2 de 90 ° par rapport à la ligne 1 et vous attendre à ce que le courant à la base de l'élément 2 soit égal en amplitude mais 90 ° en retard par rapport à celui de l'élément 1.
Ce que vous voulez, ce sont deux lignes distinctes qui fourniront l' amplitude et la phase de courant correctes à leurs extrémités de charge tout en ayant des amplitudes et des phases de tension égales à leurs extrémités d'entrée afin qu'elles puissent être jointes au point de jonction commun. Alors, comment savez-vous combien de temps pour faire chaque ligne?

Roy Lewallen, W7EL, a écrit un programme utilitaire appelé Arrayfeed1 pour effectuer les calculs nécessaires. L'utilisation de ce programme est expliquée en détail à la fois dans le fichier d'aide et dans le chapitre 8 de la 21e édition et des éditions ultérieures de The ARRL Antenna Book . Sans répéter les détails ici, vous entrez essentiellement les conditions du point d'alimentation pour chaque élément et l'impédance caractéristique (Zo) de chaque ligne d'alimentation. Le programme calculera la longueur électrique en degrés pour chaque ligne. Si vous avez entré un facteur de vélocité (VF), vous verrez également la longueur physique qui correspond à chaque longueur électrique.
En général, le programme Arrayfeed1 vous dira tout ce que vous devez savoir. Mais que se passe-t-il si vous voulez réellement visualiser ce qui se passe le long de chaque ligne ? C'est là que Zplots peut vous aider.
|
À gauche se trouve la configuration Zplots "TL FF" ( Ligne de transmission à fréquence fixe ) Générer des données pour la ligne 1. Les entrées dans la partie supérieure (à savoir une section de ligne de 75 ohms d'une longueur de 68,81 degrés électriques) correspondent aux valeurs du programme Arrayfeed1. Les entrées dans la partie inférieure (impédance de Même si vous réglez le courant à la charge, ce que vous voulez voir, c'est l' amplitude et la phase de la tension le long de la ligne. Choisir "E-mag (V)" et "E-phase (deg)" pour les sélections de trace gauche et droite produira le tableau ci-dessous. 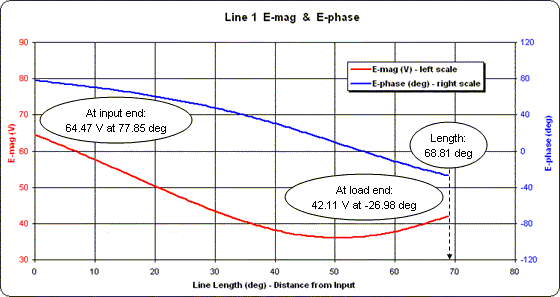
|
Bien que la longueur de la ligne soit de 68,81 degrés, l'échelle de l'axe X du graphique a été définie sur une plage de 0 à 80 degrés. Cela a été fait simplement pour fournir de beaux chiffres ronds pour les lignes de grille verticales.
À l'extrémité de charge de la ligne (vers la droite), notez que les valeurs de l'amplitude de tension (tracé rouge) et de la phase de tension (tracé bleu) correspondent à celles indiquées par EZNEC pour la source 1 à la base de l'élément 1. Suivre les deux traces pour à gauche (vers l'extrémité d'entrée de la ligne), vous pouvez voir comment l'amplitude et la phase changent.
Répéter le processus pour la ligne 2 comme indiqué ci-dessous (cette fois avec l'axe X s'étendant de 0 à 160 degrés) donne un ensemble de traces complètement différent pour l'amplitude et la phase de la tension. Mais notez que les conditions à l'extrémité d'entrée de la ligne 2 sont exactement les mêmes qu'à l'extrémité d'entrée de la ligne 1. Par conséquent, les lignes peuvent être jointes à ce point.
|

|
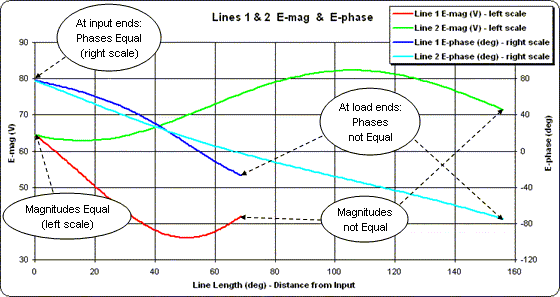
Vous pouvez utiliser le bouton "Snapshots" pour afficher les deux ensembles de traces en même temps. Autrement dit, avec les traces de la ligne 2 affichées, prenez un instantané des deux. La trace rouge sera recouverte d'un instantané vert et la trace bleue sera recouverte d'un instantané cyan (bleu clair). Puis re-tracer pour les conditions de la Ligne 1.
Cela donne une "image" de ce qui se passe. Aux extrémités d'entrée des lignes, les amplitudes de tension et les phases sont égales, de sorte que les lignes peuvent être reliées entre elles. Aux extrémités de charge des lignes, les amplitudes et les phases de tension sont complètement différentes, mais elles produisent les amplitudes et les phases de courant souhaitées nécessaires pour donner le diagramme de rayonnement correct du système d'antenne.
Comme indiqué ci-dessous, vous pouvez créer un graphique similaire pour les longueurs de ligne "2nd Solution" fournies par Arrayfeed1.
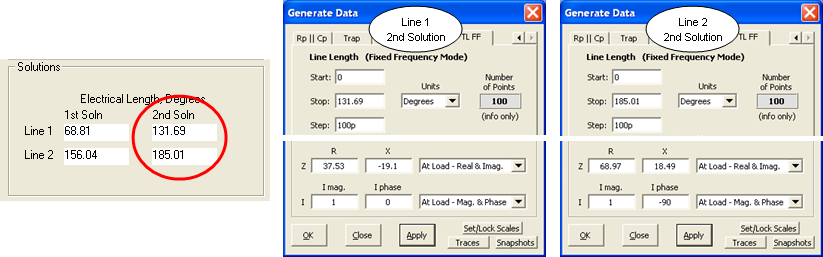

Notez que les conditions aux extrémités de charge des lignes sont identiques à la 1ère solution. Par conséquent, les mêmes courants seraient produits dans les éléments d'antenne. Cependant, cette fois, la valeur commune aux extrémités d'entrée des lignes est de 73,10 V à 109,97 degrés.
Il est maintenant temps de changer le modèle EZNEC en supprimant les deux sources de courant idéales, en ajoutant deux lignes de transmission et en ajoutant une seule source aux extrémités d'entrée communes des lignes de transmission. En fonctionnement réel, l'amplitude de la tension et du courant à la jonction commune dépendrait de la puissance fournie par l'émetteur. À des fins de modélisation, n'importe quelle valeur fera l'affaire. Dans l'exemple ci-dessous, une source de tension de 100 V à 0 degré a été arbitrairement choisie.
Cet exemple utilise également un "segment virtuel" (V1) à la jonction commune. Les segments virtuels sont une fonctionnalité d'EZNEC v.5. Si vous avez une version antérieure d'EZNEC, utilisez simplement un fil très court qui est positionné à un certain point entre les deux éléments d'antenne.


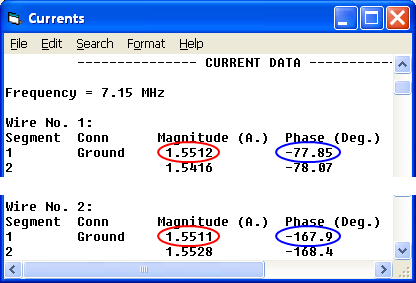
Pour vérifier le bon fonctionnement, jetez un œil à la fenêtre "Courants" EZNEC. Les amplitudes de courant (entourées de rouge) à la base de chaque élément sont pratiquement égales. Les phases (entourées de bleu) diffèrent de la quantité souhaitée, l'élément 2 étant en retard de 90° par rapport à l'élément 1.
Et pour "voir" ce qui se passe avec les courants dans les deux lignes de transmission :

Cette fois, la tension est réglée sur la valeur arbitraire commune aux extrémités d'entrée des lignes.

Le graphique de gauche a été créé en traçant d'abord les conditions de la ligne 2, en choisissant "I-mag (A)" et "I-phase (deg)" pour les sélections de trace gauche et droite, en réglant l'axe X sur une plage de 0 à 160, en prenant des instantanés, puis en traçant les conditions pour la ligne 1. (La ligne 2 a été tracée en premier simplement pour que les entrées de légende apparaissent dans l'ordre Ligne 1 - Ligne 2.)
Les amplitudes de courant (traces rouges et vertes, échelle de gauche) ont la même valeur aux extrémités de charge des lignes, comme souhaité. Les phases de courant (traces bleu foncé et bleu clair, échelle de droite) diffèrent des 90 degrés souhaités.
Tout au long de cet exemple, les longueurs de ligne ont été exprimées en unités de degrés électriques. Cela rend les longueurs valides à une seule fréquence, dans ce cas 7,15 MHz. Si vous voulez voir comment ce système d'antenne fonctionnerait sur toute la bande de 40 mètres, vous devrez exprimer les longueurs de ligne en unités physiques telles que les pieds. Le programme Arrayfeed1 peut effectuer la conversion si vous fournissez une valeur de facteur de vitesse.
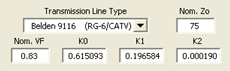
Vous pourriez être tenté d'utiliser une valeur VF "nominale" telle que 0,66 pour les lignes diélectriques en polyéthylène solide, 0,7 pour le diélectrique en téflon ou 0,83 pour le polyéthylène expansé. Mais gardez à l'esprit que le facteur de vitesse et l'impédance caractéristique Zo changent légèrement avec la fréquence. Par exemple, supposons que vous décidiez de construire vos lignes de phasage en utilisant un câble coaxial "RG-6 CATV" acheté dans un magasin Lowe's Home Improvement. Sur une plage de 1 à 100 MHz, la magnitude réelle de Zo et le VF ressemblent à ceci :
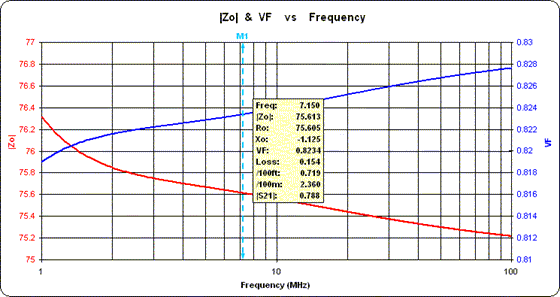
Au fur et à mesure que la fréquence diminue, remarquez comment la magnitude Zo (trace rouge, échelle de gauche) augmente de sa valeur "nominale" de 75 ohms tandis que le facteur de vitesse (trace bleue, échelle de droite) chute de sa valeur nominale de 0,83.
Pour cet exemple particulier, l'utilisation de 75,613 au lieu de 75 pour Zo dans Arrayfeed1 modifie les longueurs électriques de quelques dixièmes de degré. L'utilisation de 0,8234 au lieu de 0,83 pour VF modifie les longueurs de ligne physique de quelques pouces.

|
Vous pouvez pousser cette analyse des lignes du "monde réel" un peu plus loin si vous le souhaitez. Arrayfeed1 suppose des lignes idéales (sans perte) et des valeurs scalaires pour Zo telles que 75 ohms. J'étais curieux de voir quel serait l'effet de l'utilisation de lignes qui ont à la fois une perte et un Zo complexe, j'ai donc créé le classeur Feed2EL Excel . La capture d'écran partielle à gauche montre les résultats et voici un résumé des résultats :
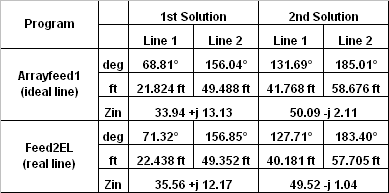
Lorsque vous utilisez des lignes "du monde réel", il y a certainement une différence dans les solutions. Mais quel effet ces différences auraient-elles sur l'amplitude et la phase du courant à la base de chaque élément ? Et comment ce système d'antenne fonctionnerait-il sur toute la bande de 40 mètres lors de l'utilisation de telles lignes ? |
Pour répondre à ces questions, la première étape consiste à modifier les spécifications de la ligne de transmission EZNEC, comme suit.

Notez que lorsque vous spécifiez des lignes de transmission avec perte avec EZNEC, vous devez utiliser la valeur Ro dans la colonne EZNEC "Z0". EZNEC calculera la valeur Xo correcte sous les couvertures.
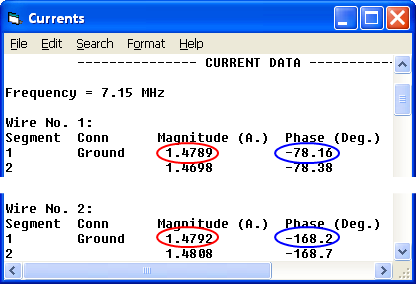
Cette fois, les amplitudes de courant (entourées de rouge) à la base de chaque élément sont légèrement plus petites en raison de la perte de ligne, bien qu'elles soient toujours pratiquement égales comme souhaité. Et les phases (entourées de bleu) diffèrent toujours de la quantité souhaitée, l'élément 2 étant en retard de 90° par rapport à l'élément 1.
Jusqu'à présent, la discussion s'est limitée à une seule fréquence, 7,15 MHz. Mais que se passe-t-il si l'antenne, désormais alimentée par des lignes de transmission ayant des longueurs physiques fixes et pertes incluses, est exploitée sur toute la bande des 40 mètres ? Et puisqu'il existe plusieurs combinaisons de longueurs de lignes d'alimentation qui produisent le même rapport de courants aux bases des éléments, quels critères faut-il utiliser pour choisir entre les solutions alternatives ? Notez que la 2ème solution (pour les lignes "du monde réel") produit une impédance à la jonction de ligne de
49,52-j1,04 ohms. Cela fournirait une correspondance presque parfaite avec une ligne de transmission standard de 50 ohms, alors pourquoi ne pas simplement utiliser celle-là ?Ce problème est abordé à la fois dans le fichier d'aide Arrayfeed1 et dans le chapitre 8 de la 21e édition et des éditions ultérieures de The ARRL Antenna Book . Essentiellement, le même libellé est utilisé dans les deux et voici une citation directe du fichier d'aide :
Bien qu'il soit tentant de sélectionner la solution offrant la meilleure adaptation d'impédance à la ligne d'alimentation principale, ce n'est pas un bon critère à utiliser. Habituellement, il est préférable de choisir la solution dans laquelle la différence de longueurs électriques entre les lignes est la plus proche du retard de phase des courants entre les éléments. Cela se traduira généralement par un réseau dont le motif et l'impédance sont moins sensibles aux variations de fréquence et de réseau physique. L'adaptation d'impédance peut être effectuée au point d'alimentation principal si nécessaire.Pour la 1ère solution, la différence entre les longueurs de ligne est d'environ 85 degrés. Pour la 2ème solution, c'est environ 55 degrés. Voyons donc comment les deux solutions fonctionnent sur toute la bande des 40 mètres.
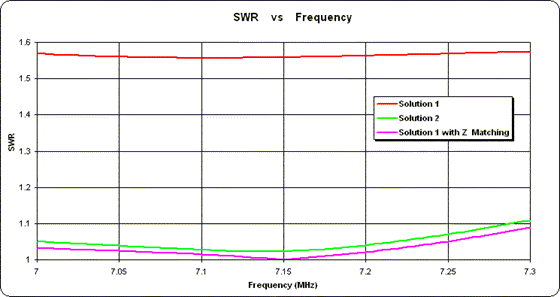
Effectivement, le SWR pour la solution 1 (trace rouge) est assez plat sur toute la bande. La solution 2 (trace verte) n'est pas aussi plate mais (dans ce cas) montre des valeurs globales inférieures. Et bien que l'un ou l'autre soit tout à fait acceptable dans la pratique, juste à titre d'illustration, j'ai ajouté un simple réseau d'adaptation d'impédance entre le point de jonction de la solution 1 et la ligne d'alimentation principale. La réponse SWR pour cette combinaison est indiquée par la trace magenta.
J'ai utilisé un simple réseau L pour l'adaptation d'impédance, mais vous pouvez faire la même chose avec un transformateur de ligne de transmission à section série, une correspondance de bout ou diverses autres techniques. Voir le chapitre 26 du livre des antennes ARRL pour plus de détails.
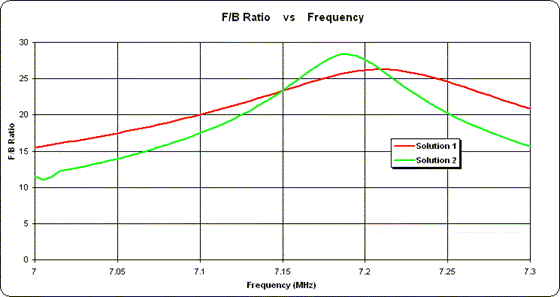
La vraie différence entre les solutions apparaît dans le modèle. Bien que le gain direct soit presque le même dans les deux cas (et ne sera pas montré ici), le rapport F/B est à nouveau plus plat pour la solution 1.
Notez que l'inclusion d'un réseau L d'adaptation d'impédance à la jonction n'a aucun effet sur le modèle. Il n'est pas nécessaire d'afficher une troisième trace (magenta) car elle est exactement la même que la trace rouge.
Si vous souhaitez expérimenter une analyse similaire à celle ci-dessus, les fichiers de modèle EZNEC (.ez) sont disponibles sur Sample Feed2EL Models.zip . Notez que la plupart des modèles utilisent des segments virtuels, une ligne de transmission avec perte et/ou des réseaux L. Ils doivent donc être utilisés avec la version 5 d'EZNEC.
C'est intéressant et éclairant de faire des études théoriques comme celle-ci mais ça ne sert à rien d'aller trop loin avec la précision. Rappelez-vous que tout est basé sur les valeurs d'impédance aux points d'alimentation pour chaque élément. Même les meilleurs modèles seront probablement décalés d'au moins quelques ohms. La seule façon de savoir avec certitude est de faire des mesures réelles pendant que l'antenne est en fonctionnement. Le chapitre 8 de The ARRL Antenna Book décrit les méthodes pour y parvenir.
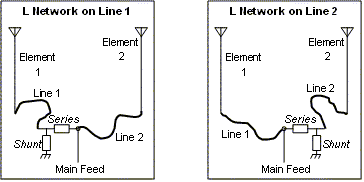
Avant de terminer cette discussion sur les lignes de phasage, il y a un autre élément à mentionner. Une autre méthode pour alimenter les deux éléments de l'antenne décrite ci-dessus consiste à utiliser un réseau L pour fournir le retard de phase nécessaire, puis deux lignes de transmission quart d'onde "à forçage du courant" pour alimenter les éléments. (Notez que ce réseau n'est pas le même que le réseau L mentionné précédemment. Celui-ci était pour l'adaptation d'impédance et a été inséré à la fin de la ligne d'alimentation principale. Celui décrit ici est pour le déphasage, pas l'adaptation d'impédance, et est inséré avant l'une ou l'autre des lignes "forçage courant".)
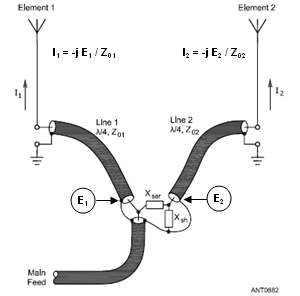
Cette méthode d'alimentation alternative est illustrée à gauche dans une illustration de The ARRL Antenna Book (Fig 17 aux pages 8-19 de la 21e édition, avec une annotation supplémentaire ajoutée). Le réseau L, composé de la réactance série X ser et de la réactance shunt X sh , fournit un rapport souhaité entre les tensions E 1 et E 2 . L'action des lignes de transmission "forçage de courant" reproduit alors ce même rapport dans les courants à la base des éléments respectifs, en supposant Z 01 égal à Z 02 .
Pourquoi donc? Et à quoi « ressemblent » les amplitudes et les phases de tension et de courant sur les lignes de transmission ?
D'abord les maths. L'équation générale (Terman, Radio Engineers' Handbook et autres) reliant la tension à l'extrémité d'entrée d'une ligne à la tension et au courant à l'extrémité de charge est :
Ein = Eload * cosh(gamma*len) + Iload * Zo * sinh(gamma*len)où:Ein = Tension à l'entréeLa constante de propagation complexe gamma est composée d'une partie réelle, alpha, et d'une partie imaginaire, bêta. C'est-à-dire:
Eload = Tension à la charge
Iload = Courant à la charge
Zo = Impédance caractéristique de la ligne
gamma = Constante de propagation de la ligne
len = Longueur de la ligne
Notez que toutes les grandeurs sauf la longueur de la ligne sont complexes.gamma = alpha + j bêtaoù:alpha = constante d'atténuation, népers par unité de longueurLes fonctions hyperboliques complexes cosh(gamma*len) et sinh(gamma*len) peuvent être décomposées en une séquence de fonctions scalaires comme suit :
bêta = constante de phase, radians par unité de longueurcosh(gamma*len) = cos(beta*len) * cosh(alpha*len) + j (sin(beta*len) * sinh(alpha*len)) sinh(gamma*len) = cos(beta*lenPour une ligne sans perte, l'atténuation est de 0, donc alpha*len vaut 0. Pour un quart de longueur d'onde, beta*len vaut pi/2 radians ou 90 degrés. Ainsi les développements cosh(gamma*len) et sinh(gamma*len) deviennent :
) * sinh(alpha*len) + j (sin(beta*len) * cosh(alpha*len))cosh(gamma*len) = cos(90°) * cosh(0) + j (sin(90°) * sinh(0)) = 0 * 1 + j (1 * 0) = 0 + j0 sinh(gammaDonc:
* len) = cos(90°) * sinh(0) + j (sin(90°) * cosh(0)) = 0 * 0 + j (1 * 1) = 0 + j1Ein = Echarge * (0 + j0) + Icharge * Zo * (0 + j1)En divisant les deux côtés par j et en divisant les deux côtés par Zo, on obtient :
= j * Icharge * ZoIload = -j * Ein / ZoAinsi, tant que la ligne a une atténuation nulle et que la longueur est précisément de 90 °, le courant à la charge dépendra uniquement de la tension à l'entrée et de l'impédance caractéristique de la ligne. De plus, la phase du courant de charge sera décalée de 90° précisément par rapport à la phase de la tension d'entrée. Le courant à la charge ne dépend pas de l'impédance à la charge. Par conséquent, si deux charges différentes sont alimentées via deux lignes de transmission sans perte d'une longueur précise de 90 ° avec la même tension aux extrémités d'entrée des lignes, ou avec des tensions d'entrée ayant un rapport connu, alors le courant à travers les deux charges sera identique, ou sera ont le même rapport que les tensions d'entrée, quelle que soit l'impédance de chaque charge.Notez que vous pouvez également profiter de cette propriété des lignes à 90° pour mesurer le courant à la charge. Autrement dit, si vous connaissez la tension à l'extrémité d'entrée de la ligne ainsi que l'impédance caractéristique, et que vous savez que la perte de ligne est négligeable, alors en mesurant la tension à l'entrée, vous pouvez facilement calculer le courant à la charge.
Eh bien, "facilement" si vous travaillez avec de beaux nombres ronds et que vous pouvez convertir du polaire au rectangulaire et revenir au polaire dans votre tête et que vous pouvez garder le "-j" droit. Sinon, il pourrait être plus pratique de laisser un ordinateur faire le calcul.

|
À gauche, vous pouvez configurer le panneau "TL FF" pour une ligne de "forçage de courant". Pour cet exemple, nous ne nous intéressons pas à ce qui se passe le long de la ligne, nous ne nous soucions que des extrémités d'entrée et de charge. Définissez donc le nombre de points calculés sur 2, appuyez sur OK, puis tabulez sur la feuille de données du classeur Zplots .

La longueur 0 est l'extrémité d'entrée de la ligne, la longueur 90 est l'extrémité de chargement. L'amplitude du courant de charge est de 1,333 (c'est-à-dire D'autre part, si vous aviez spécifié une "vraie" ligne telle que le "Lowe's Home Center RG-6 CATV" (qui, à partir de mesures réelles, est similaire à Belden 9116) comme suit :
Ensuite, vous verriez:

Lorsque la perte de ligne est incluse (ce qui signifie également que Zo est complexe), les résultats sont toujours proches mais ne sont plus précisément liés à la tension d'entrée. Au lieu de cela, les calculs complets du sinus et du cosinus hyperbolique donnent les résultats indiqués. |
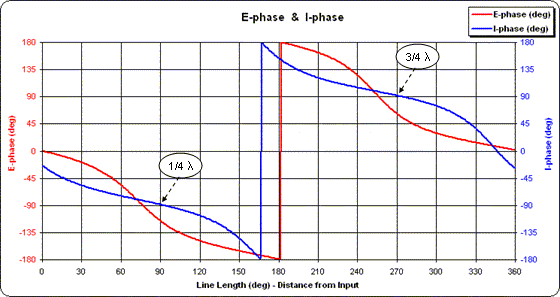
Enfin, à quoi « ressemblent » les choses le long de la ligne ? Les deux graphiques suivants comparent la tension et le courant le long de la ligne en utilisant le deuxième scénario ci-dessus, c'est-à-dire avec une ligne "réelle" par opposition à une ligne sans perte idéale. De plus, la longueur de la ligne a été allongée de 90° à 360° tout en conservant les mêmes conditions à l'extrémité d'entrée de la ligne. Notez la similitude de l'amplitude du courant (environ
100/75 ou 1,3 A à la fois à 90° et 270°) par rapport à la phase du courant à ces deux points (environ -90° et +90°).

|
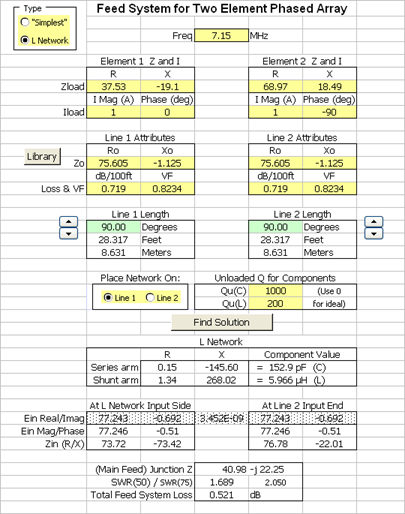
Le système d'alimentation de type réseau L est également inclus dans le classeur Excel de Feed2EL . En plus d'utiliser des lignes d'alimentation "du monde réel", les effets de la perte de composant peuvent également être inclus en spécifiant les facteurs Q du condensateur et de l'inductance. Les deux lignes d'alimentation ne doivent pas nécessairement avoir une longueur de 90 °, sauf si vous souhaitez mesurer indirectement le courant de l'élément en mesurant la tension (peut-être avec un oscilloscope) à l'extrémité d'entrée de la ligne, comme mentionné ci-dessus. Et vous pouvez placer le réseau sur la ligne 1 ou la ligne 2.
Comme avec le système d'alimentation "le plus simple", ce n'est probablement pas une bonne idée de prendre une décision basée uniquement sur la valeur SWR. Au lieu de cela, vous voudrez peut-être regarder les valeurs de réactance pour les composants du réseau L. Par exemple, la capture d'écran à gauche montre les valeurs lorsque le réseau L est placé devant la ligne 1 et ci-dessous sont les valeurs si le réseau est placé devant la ligne 2.
Notez que dans ce cas particulier la valeur de l'inductance est beaucoup plus faible si le réseau est placé sur la ligne 2. |
En utilisant EZNEC v.5, vous pouvez modéliser le réseau L comme ceci.
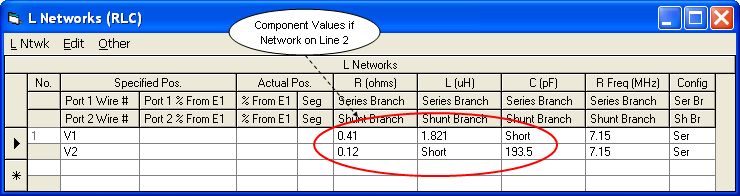
Lors de la création de réseaux en L avec EZNEC, n'oubliez pas que la branche de série est toujours saisie en premier, que le réseau " soit orienté " vers la gauche ou vers la droite.
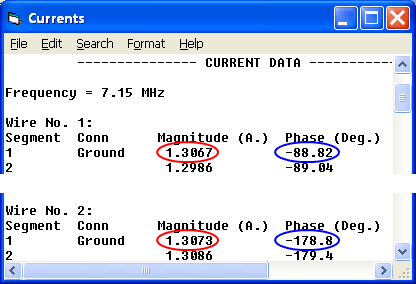
L'exécution du modèle, puis la vérification des courants vérifient que le réseau fonctionne comme prévu. Bien que les lignes d'alimentation aient toutes deux la même longueur (dans ce cas 90°), le réseau a effectué la transformation de tension correcte à l'extrémité d'entrée de la ligne 2 de sorte que les courants aux bases des éléments aient la relation souhaitée.
(Ce fichier de modèle EZNEC est inclus dans Sample Feed2EL Models.zip .)

Comme c'était le cas avec les solutions « les plus simples », il y a une nette différence dans le modèle de rapport F/B lorsqu'un balayage est effectué sur toute la bande de 40 mètres. Cependant, à la fréquence de conception de 7,15 MHz, le rapport F/B est exactement le même dans tous les cas, ce qui vérifie que les conceptions ont été réalisées correctement.